Learn basic math on line

Understanding the history of mathematics

Children will likely learn their basic math skills in school but most K-12 curriculums overlook the history of mathematics itself. This subject may prove especially helpful to a child experiencing challenges in math, as they will see that the subject has been a culmination of years of hard work and discovery, a process built upon by bright and industrious individuals.


The term “mathematics” originates from Greek root words that tell us that the subject, at its heart, is about learning, not about numbers. Mathematics did not develop out of idleness and boredom but instead out of a human desire for organization, a need to measure, calculate, estimate, and make everyday activities more efficient. The counting of basic supplies and necessities- crops, food and animals - led to the more complex counting of time, eventually leading to days, seasons and years. As human civilizations developed and grew, so did the need for math. Every science relies upon basic mathematical rules in its practice.


Each culture has had its own important developments in mathematics. Babylonian mathematicians, working in 2000 B.C.E., developed theories that were later tested and built upon by dedicated Greek thinkers. Indian mathematicians working from 1500-1600 C.E. developed the concepts of zero and infinity as well as negative, irrational, and binary numbers. The Arab countries were known to use three different types of counting systems in the eleventh century: finger-reckoning arithmetic, the sexagesimal system, and the Indian numeral system. The finger-reckoning system had numbers written in words and counting done on fingers. The business community prevailing at that time made extensive use of this system. The sexagesimal system used numerals denoted by letters of the Arabic alphabet and was primarily used by Arabic mathematicians for astronomical work while the Indian numeral system utilized Indian numerals and fractions with the decimal place-value system allowing most of the advances in numerical methods by the Arabs.


While mathematics continued to progress throughout Greece and later in Europe, the efficiency with which math was calculated improved as well. Mathematical symbols became more organized, allowing for new and important discoveries in the field. Your children should understand that mathematics was born out of necessity, developed out of curiosity and a desire for efficiency, and was perpetuated by teamwork.

1. Find the value of the function x3+2x+5 at x=2
a) 17
b) 15
c) 18
d) 19
2. 7n2-7n+5-(3n+7n2)=
a) 5+10n
b) -10n+5
c) 10n-5
d) 45-10n
3. If a=3,b= - 1,c=2,which is true.
I. a+b+c
II. 3a+5b=4
III. 2c-5a=6
a) 1 only
b) 2 only
c) 3 only
d) 1 and 3
e) 1 and 2
4. If x2-y2=58 and x-y = 4, what is the average of x and y?
a) 13
b) 27
c) 2
d) 3.6
5. If a2-b2 = 21 and a2+b2 =29, which of the following could be the value of a?
a) 10
b) 5
c) 0
d) none of above
6. If 12/m = 15/m2, then m =?
a) 5/4
b) 3/5
c) -5/3
d) -3/5
e) none
7. If x = (p+q) / (p-q), then x-1 =?
a) q/p-q
b) 2q/(p+q)
c) 2p(p-q)
d) 2q/(p-q)
8. If p+q = 4,q+r =-2,r+p=3,then p+q+r =?
a) 2/5
b) 5/2
c) 6/2
d) 5
e) 6
9. If 5a=2b=40c, what is the value of8a=5b in term of c?
a) 10c
b) 164c
c) 52c
d) 25c
10. If p = 10/ (q+2), what is the value of pq in terms of p?
a) 2(5-p)
b) 10/p
c) 3(p-5)/p
d) 2(p-5)/p

A set is generally described as a well defined collection of distinct objects.By a well defined collection is meant a collection which is such that,given any object,we may be able to decide whether the object belongs to the collection or not.By distinct objects we mean objects objects no two of which are identical.
Elements or members of set:
The objects in a set are called its members or elements.Capital Letters A,B,C,X,Y,Z etc.,are generally used as names of sets and small letters a,b,c,d,x,y,z etc are used as members of sets.
E.g N = The set of all natural numbers = {1,2,3,...}
      W= The set of whole numbers = {0,1,2,3,...}
Ways of describing a set:There are three different ways of describing a set
1.The Descriptive Method:
A set may be described in words.for example,the set of all vowels of English alphabets.
2.The Tabular Method:
 A set may be described by listing its elements within brackets
{a,e,i,o,u}

Fraction is an expression in which we can write a number in the form P(x)/Q(x) , where Q(x) does not equal to zero.

we can check which fraction is smaller and which is greater.If the fractions has same denominator,then which fraction has greater numerator is the greater fraction.and which fraction has smaller numerator is the smaller fraction.
E.g: 4/5,6/5,3/5
In the above example 6/5 is the greatest fraction.and 3/5 is the smallest fraction.
If the fraction has different value of denominator then 1st we take two fractions,putting them equal and using cross multiplication ,then which side is greater is the greater fraction and which side is smaller is the smaller fraction.

the numbers or expressions written above the line in a fraction are called numerator

Rationalization:A fraction is to be rationalized if the denominator contains irrational numbers or complex numbers.that irrational number may be multiplied top and bottom of the fraction.

Trigonometry contains three words:
Tri means three
Goni means angle
Metron means measurement

Linear equation:an equation of the form ax+b = 0,where a doesn't equal to zero is called linear equation.
Its graph is a straight line.

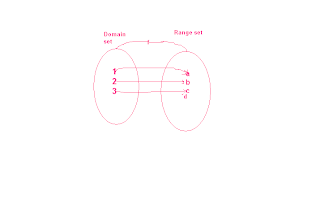
Onto function:A function in which range of function is equal to the range set are called onto function.

Angle:Two rays with a common starting point form an angle.One of the ray is called initial ray and other is called terminal ray.

Circular system :A system in which we discuss about radian is called circular system.
Radian is the measure of an angle at the centre of circle by an arc whose length is equal to the radius of circle

The terms below the line of a fraction are called denominator.

there are two types of fraction:
1: Proper rational fraction:A fraction in which degree of numerator is less than the degree of denominator are called proper rational fraction.
E.g (x-1)/(x-2)(x-3)

2:Improper rational fraction:A fraction in which degree of numerator is greater than or equal to the degree of denominator are called proper rational fraction.

E.g (x-1)(x+3)/(x-2)(x-3)

3:Mixed fraction:

The sum of a whole number and a proper fraction is called mixed fraction. That sum is implied without the use of any operation such as "+"; for example, in referring to two entire biscuit and three quarters of another biscuit, the whole and fractional parts of the number are written next to each other:    .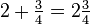

Rational numbers are those numbers which can be written in the form of p/q where
q ≠ 0.
For example:All real numbers are also called rational numbers.
In other words" we can say that there in no gape between real numbers".
In real numbers,there is no number exist between two consecutive real numbers ,while in rational numbers there may exist infinite many numbers between two rational numbers.

A prime number which can be divisible by 1 and the number itself.  
1 is not a prime number because in the case of 1,one property is repeated.
that is why we can not say that 1 is a prime number.

   Even Numbers:the numbers which are divisible by  2 are called even numbers.Examples are : 0,2,4,6,8,... etc
odd numbers: the numbers which are not divisible by 2 are called odd numbers.

• positive numbers
• negative numbers
• non negative numbers
  Positive numbers are those numbers using with positive sign:the numbers such as 1,2,3...etc.are named as positive numbers.
• negative numbers are those numbers using with negative sign.:the numbers such as -1,-2,-3...etc are called negative numbers.
• Non negative numbers are those numbers which include zero along with positive numbers.

Gre test has become a very famous among students.To pass a test like Gre is as to climb up on mount Everest.
Test math (G.R.E) and (N.T.S)
1. What is the length of a rectangle that has width 10 and perimeter 60?

a) 15

b) 25

c) 20

d) 40

2. If 2x = 7 and 3y =2, then9xy?

a. 14

b. 18

c. 21

d. 28

e. 63

3. If 0.768 = x/100, then x is closet to which of the following?

a) 0.77

b) 0.80

c) 8

d) 76

e) 77

4. SAM ate ¼ of a whole pizza and Jane ate 1/5 of the remaining portion. What fraction of the pizza was not eaten?

a. 11/20

b. 9/20

c. 3/20

d. 3/5

e. 2/5

5. If x =2 and y = - 2 then 2x – 2y =?

a. – 8

b. 0

c. 4

d. 6

e. 8

6. What value of x satisfy the equation x – 1 = 1 – x?

a. 2

b. 1

c. 0

d. – 2

e. None of these
7.    If 25 percent of a certain number is 1640.what is 10 percent of a number?